Scalable,transparent, and post-quantum secure computational ==> https://eprint.iacr.org/2018/046.pdf 部分内容翻译:
0 介绍
可扩展式验证的计算完整性,超过密文数据集
本文讨论的问题基于如下假设:想象警察 Police(P) 是负责国家法医DNA档案数据库 database(D),声称一个即将任命(或者据称可能发生腐败案)的DNA档案文件 profile(p)没有出现在D中。加密协议能否说服怀疑者相信警察的声称,并且不进入D或p,不依赖于任何外部信任方(例如,首席大法官)和具有”合理”计算资源?
DNA配置文件匹配 (DNA profile match, DPM) 示例是一个普遍问题的特殊情况。某一方(party, P)在数据集(D)上执行计算(C)能会有错误报告,而不是正确输出 (C(D)),提出了计算完整性问题 (computational integrity ,CI),以确保P确实报告C(D)。当数据集 D 是公开时,任何有兴趣验证 CI 的一方 (verifier, V) 都可以在 D 上重新执行 C 并将其输出与 P 报告输出进行比较,因为客户可能会检查餐厅账单,或作为一个新的比特币节点将验证其区块链。此原始的解决方案无法扩展,因为验证器 (Tv)花费的时间与执行程序 (Tc)所需的时间一样大,V 必须读取完整的数据集D。基于加密哈希函数的承诺方案常用于计算大型数据集 Dt,t 时刻状态的”指纹”哈希为cmt。通常,与 Dt 相比,cmt 的长度可以忽略不计,作为公告可以很容易地张贴在块链上。但是,CI 的方案中,我们希望解决扩展性问题,也就是增加参数和计算深度的问题,其中验证时间和计算复杂度近似于 logTc 和 |cmt|(cmt的bit长度),而不是 Tc 和 |Dt|;至少 验证时间/通信 应该严格小于 Tc 和 |Dt|。
当数据集 D 包含机密数据时,无法再实现原始的解决方案,并且负责D的P方可能以保密的面纱隐瞒违反计算完整性的行为。当对机密数据强制实施 CI 的方法则依赖于”受信任方”,例如审计师或会计师代表公众验证计算。此解决方案不提供可扩展,就像数据公开的方案一样。更糟糕的是,它要求公众信任第三方,这创造了一个潜在的协议中的失败点,因为第三方可能违反协议,如收到恶意方贿赂或胁迫。
零知识(ZK)证明和论证系统是取代人工审核员的自动化协议。为了保证计算完整性同时基于机密数据,实现有效的计算,消除腐败并降低成本。ZK系统中,S和计算C是一对随机算法,S=(P, V);证明人 P 是用于证明计算完整性的算法;验证人 V 检验这样子的证明(proofs)。S 的完整性和健全性意味着 P 可以有效地证明所有真相,但无法说服 V 任何谬论。关于 ZK 系统针对通用计算的可扩展式验证,最早出现在1990年代,基于 Probabilistically Checkable Proofs (PCP) 这一篇论文。PCP 定理提供了一种平衡,证明人构建证明花费的时间(Tp)和验证人验证的时间(Tv)的平衡。这种平衡意味着生成证明的时间多项式式增加(Tp=Tc多项式),同时验证时间指数式增加(Tv=logTc多项式)。
基于PCP定理(ZK-PCP)的ZK系统具有三个附加优点,这使得公众信任计算完整性至关重要。
(一) 这些构建安全的假设被建造起来了。即交互式解决方案具有抗碰撞哈希函数,非交互式函数具有对随机函数(“随机预言模型”) 的通用访问权限,这些理论基础在目前认为还不会受到大型量子计算机的影响,我们称之为后量子安全(post-quantum secure)。量子计算机规模以及对后量子密码协议的需求都在增长,如,美国国家标准与技术研究院技术(NIST)强调了后量子安全ZK解决方案的重要性。
(二) ZK-PCP是知识证明(proof of knowledge, POK)系统,或者当如上所述实现时,是知识论证(argument of knowledge, ARK)系统。非正式地,在DPM示例的背景下,ZK-ARK是一个证明,使公众相信警察已经使用了“真实的”数据集Dt和总统候选人DNA配置文件p,总统候选人的承诺是先前已经宣布过的。
(三) 最重要的是,ZK-PCP是透明的 (或“公共随机性”),这意味着验证者使用的随机性是公共的。特别是,与更加新一些的ZK解决方案(包括Zcash加密货币使用的解决方案)相比,ZK-PCP不需要外部受信任的设置阶段。透明性对于能否取得公众信任至关重要,因为它限制了当事人P滥用系统的能力,因为,只要在可观察的宇宙中存在不可预测的事物,透明的系统就是公众可能会信赖的系统。
综上所述,ZK-PCP是确保公众对机密数据CI信任的最佳方法,并具有六项核心优点。
(一) 透明性;
(二) 普遍性—适用于任何有效的计算C,即使它需要上述Dt之类的辅助输入;
(三) 机密性,即零知识性(ZK)—请勿破坏Dt等辅助输入;
(四) 后量子安全;
(五) 基于知识的证明(或者论据);
(六) 可扩展的验证。
虽然 ZK-PCP在上个世纪90年代已经被知晓,但并没有被实现,因为“PCP定理产生的证明既漫长又复杂,以至于要花费数千年的时间来生成和检验它们,并且将需要比宇宙中原子更多的存储位”。ZK系统在为通用计算的努力过程中,仍没有完全实现 (一) — (六) 的替代技术上,尽管某些算法对于某些具体的电路尺寸和计算开销是有效的。
1 本文的主要贡献
我们在IOP(Interactive Oracle Proofs)模型中提出了一个(双重)可扩展和透明的ZK系统的新结构(Scalable Transparent IOP of Knowledge, ZK-STIK)。我们将该系统实现为ZK-STARK,并将其应用于概念验证POC“有意义”的计算,该计算本质上是高度顺序的,如前面介绍的DPM问题。我们实现了如下两点:
(一) 验证时间严格小于原始运行时间 (Tv<Tc)
(二) 通信复杂度严格小于见证人大小
本系统中核心创新和改进性能的主要来源是对IOP模型的扩展,包括快速FRI (Fast Reed-Solomon (RS) IOP of Proximity (IOPP)) 协议,这里的IOP是 Interactive Oracle Proofs,还有一个新的算法规程。我们强调,验证时间和验证大小适用于为任意见证者定义的任何计算,尽管加速实现的具体点取决于计算的复杂性。
DNA档案匹配计算
ZK-STARK是一个“有意义”的概念验证(POC),特别适用于DNA档案匹配问题(DNA profile match (DPM))。该计算做出了以下场景假设:假设警察(充当证明人P)负责国家法医DNA档案数据库(D),并且在先前时间的t,发布数据库状态Dt(例如,在区块链上)隐藏承诺cmt。警察现在声称,即将任命的和据称腐败的总统候选人的DNA档案p没有出现在Dt中,因此希望以可扩展的方式创建一个有说服力的证据,使得公众认为DPM计算正确无误,并且警方报告的输出(关于p和Dt)是正确的。
在超过50个国家/地区中使用的DNA图谱的主要标准是联合DNA索引系统(CODIS)格式; 根据该标准,个人由其DNA的短串联重复序列(STR)表示,针对一组20个“核心基因”进行了测量。假定对CODIS数据库状态Dt的承诺(commitment) cmt是公共信息(如,在时间t,公开于区块链之上),对于总统候选人简历p的承诺是cmp。我们假设p是由独立实验室提取的,然后在公开发布cmp时将其(秘密地)交给了警察。 假设警察宣布:
“该值a是在具有承诺cmt的数据库中,对具有承诺cmp的档案文件进行匹配搜索的结果”
答案是三种可能性之一:“不匹配”,“部分匹配”或“完全匹配”。公开(开源)计算C是将由可信任的第三方执行的用于验证上述声明的计算。此计算需要三个公共输入(cmt, cmp和A),以及两个机密输入:DNA文档数据库D’和个人DNA文档文件p’。当且仅当公共输入(cmt, cmp, A)和机密输入(D’, p’)满足以下三个条件时,计算C则成功终止:
(i)针对机密输入D’的承诺cm’与公开输入cmt相等;
(ii)针对机密输入p’的承诺cmp’与公开输入cmp相等;
(iii)在机密数据集D’中对机密输入p’进行匹配搜索后,得到输出则会公开宣布结果a.
令|D(n)|为数据集D(n)的比特长度,n为DNA档案的条目数量(每条档案为40字节长度)。令CC(n)为ZK-STARK的通信复杂度,数据集仍然为D(n),例如,在证明人与验证人之间,总的通信比特值。令Tc(n)为原始验证计算C在D上执行时,数据量为n时,所耗费的时间。令Tv(n)为V验证所耗费的时间。以上时间是同为一台物理服务器上测试所得。
2 讨论 — 权力下放的社会职能的应用
以比特币为首的加密货币通过建议完全分布式的货币体系来代替法定货币,加密货币同时正在破坏已建立的金融系统。 金钱只是可以分布式的社会功能之一,法律合同已经被以太坊区块链中的自动智能合同取代。 在本节结束时,我们将讨论ZK-STARK系统对分散式公共分类账的两个预期影响。
可扩展性
现如今,在区块链中进行了激烈的讨论,围绕着适当的方式来扩展交易吞吐量,而又不会增加参与网络的节点的时间和空间。正如其中一位作者首次指出的那样,并且最近被数种加密货币计划所采用,完全可扩展的证明系统(即使没有零知识)也可以通过成倍地减少验证时间来解决可扩展性问题。更详细地讲,单个“证明人节点”可以在准线性时间内生成一个证明,该证明将说服其他节点接受账本当前状态是有效的,而无需那些节点原始地重新数据库查询计算,也不需要存储整个区块链的状态。
隐私性
ZK证明的保密性已被用于增强加密货币的互换能力和隐私能力。最近在Zcash加密货币中实现并使用一种特殊的零知识证明,即ZK-SNARK,它基于密码学指数知识(knowledge of exponent, KOE)的假设,以完整地维护其条目的分布式注册表,该注册表隐藏着未动用资金的承诺。
ZK-SNARK(zero-knowledge succint non-interactive arguments of knowledge。Zero knowledge:零知识证明;Succinctness:证据信息较短,方便验证;Non-interactivity:无交互,证明者基本上只要提供一个字符串义工验证。对于区块链来说,这一点至关重要,意味着可以把该消息放在链上公开验证;Arguments:证明过程是计算完好(computationally soundness)的,证明者无法在合理的时间内造出伪证(破解)。跟计算完好对应的是理论完好(perfect soundness),密码学里面一般都是要求计算完好;knowledge:对于一个证明者来说,在不知晓特定证明 (witness) 的前提下,构建一个有效的零知识证据是不可能的。
ZK-SNARK是不是透明的,因为它们需要一个“设置阶段setup phase”,该阶段使用了非公开的随机性,如果受到损害,则可以用来损害系统的安全性。展望未来,ZK-STARK可以替代ZK-SNARK,透明地实现Zcash的可替代性和机密性。当前,ZK-SNARK比ZK-STARK证明size小约1000倍,因此用ZK-STARK替换ZKSNARK还需要进行更多的研究以缩短证明长度,或者使用可增量验证的计算来汇总和压缩多个ZK-STARK证明。例如,ZK-SNARK的证明size为几百bytes,ZK-STARK的证明size为几百Kbytes。
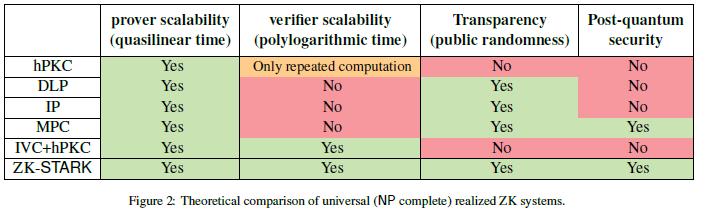
3 与其他的ZK系统相比较
hPKC — Homomorphic public-key cryptography 同态公钥密码,如Pinocchio和libSNARK。
DLP — Discrete logarithm problem 离散对数问题,如BulletProofs。
IP — Interactive Proofs 交互式证明。如Hyrax。
MPC — Secure multi-party computation 多方安全计算。如ZKBoo、Ligero。
IVC — Incrementally Verifiable Computation 增量可验证计算。如hPKC-based IVC。
具体测试指标
测试均基于同一个硬件服务器,基于同样的DPM问题。
Arithmetic circuit complexity as standard measuring yard — 算术电路复杂度作为标准测量场。此处测试的所有系统(包括ZK-STARK)均为算术化之后的运算,将计算完整性(CI)语句简化为相关的有限域上的低次多项式系统。我们强调ZK-STARK也可以在素数场上运行,但代码中尚未实现。
在DPM计算中,数据库中具有n条数据,算术电路的参数如下:
电路深度 depthn = 62·n
电路宽度 w = 81
验证复杂度 witn = 40·n bytes
乘法复杂度 multn = 1467·62·n ≈ (2^16.4)·n
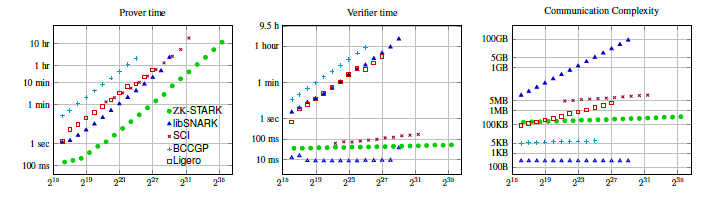
我们对ZK-STARK系统(证明方+验证方)进行了测量,本ZK-STARK具有60位(bits)的安全性,即n最大值≈60。libSNARK、SCI具有80位的安全性。BCCGP具有128位。Ligero具有60位的安全性。我们预估80位证明者的证明时间比60位最多长5%。如果您看到下图,则它们还包括一个没有setup的libSNARK线,并且明显位于ZK-STARK线之下。
总结
在上述以对照的方式进行测试,ZK-STARK是测量的所有电路尺寸中生成证明最快的,特别是与libSNARK相比较,速度快了近10倍。在小电路情况下,ZKBoo和Ligero的通信时间更短,验证更快。在深度较小的电路的情况下,Hyrax的通信时间更短,验证更快。在同一固定电路上多次重复的计算,BulletProofs, Pinocchio, libSNARK的通信时间更短,验证更快。但是,对于一般的大规模计算,ZK-STARK的验证时间和通信复杂性优于其他透明系统。换句话说,我们对ZK-STARK的实践表明,对于实际相关的具体计算(例如DPM),已经充分体现了完全可伸缩性和透明性的优势,并表明我们的系统类型对于构建可伸缩性解决方案很有用, 例如,用于分布式的加密货币。