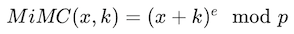学习笔记 ==> https://www.youtube.com/watch?v=4ENECj3Jw24&t=1s https://docs.iden3.io/protocol/spec/
Round0: 简介 本文将由浅入深地解读Iden3项目,希望读者读完后,完全理解 iden3的原理和did的精髓,并能够上手使用Iden3开发项目。为什么要做一次Iden3的介绍?笔者很早就研究过did协议,也做过一些粗浅的开发,但是这次使用iden3开发了一整套应用,期间被迫把几乎所有文档和代码都反复研读了几遍。过程虽然痛苦,但对did的理解变得深刻了许多。因此,向各位做一次分享汇报,同时也作为自己的学习笔记。由于脑子一直不太好使,难免有理解的不到位的地方,还希望各位多多交流。
Round1: 应用 背景:什么是DID Iden3是一套Did协议的实现,允许使用者使用其提供的sdk构建did应用,并满足w3c did标准的基本语义,包括可验证声明、选择性披露等。如果您不熟悉did协议,可以参考w3c did协议,Dapp Learning也做过相关的讲解,可以参考。如果您没有时间阅读did的知识,就目前而言,您只需要记住如下几个要点:
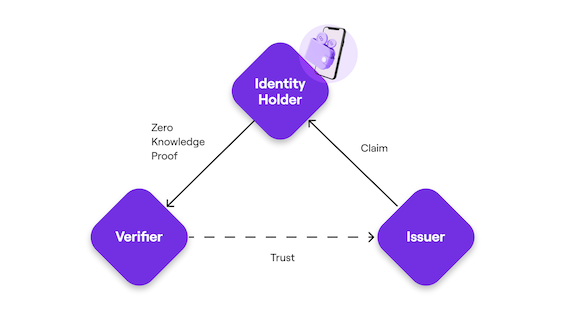
did包括三个角色:issuer,holder,verifier。
issuer负责分发claim给holder,claim里面包含各种holder的信息,换言之记录了“谁有什么属性”。例如,issuer如果是政府机构对的话,claim则可以是身份证,上面记录了姓名、证件号码、出生日期等描述公民的信息;而holder则看作公民,verifier可以是机关单位、商业场所等,他们可以要求公民提供证件的有效信息。
当claim可以向holder提供关于自己claim数据的证明,一方面证明自己确实拥有issuer提供的claim,一方面证明claim满足某些条件。这种证明也被称为credential。出于隐私保护的要求,credential通常具有选择性披露性质,只证明自己持有必要的属性,例如最经典的,仅根据身份证上的出生日期,判定自己大于18岁。
issuer、holder、verifier之间使用公钥来认证彼此。这个公钥存储在did doc中,而did doc将锚定到去中心化设施上。最简单的理解方式是认为did doc存储在链上,尽管实际上一般是链下存储具体数据,链上存摘要的形式。
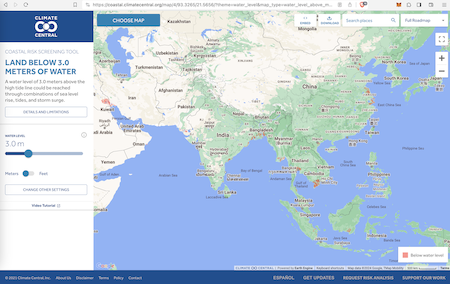
应用体验:PolygonId 目前,基于Did协议构建的最典型应用是polygon id,根据官网的描述,它将是polygon接下来要主推的产品。用户可以访问它的test版本,在上面方便地注册、分发凭证。本文以polygon ID为例,讲解iden3的架构。
注册issuer 首先点开polygon platform:https://devs.polygonid.com/docs/quick-start-demo/ , https://user-ui:password-ui@issuer-ui.polygonid.me/schemas
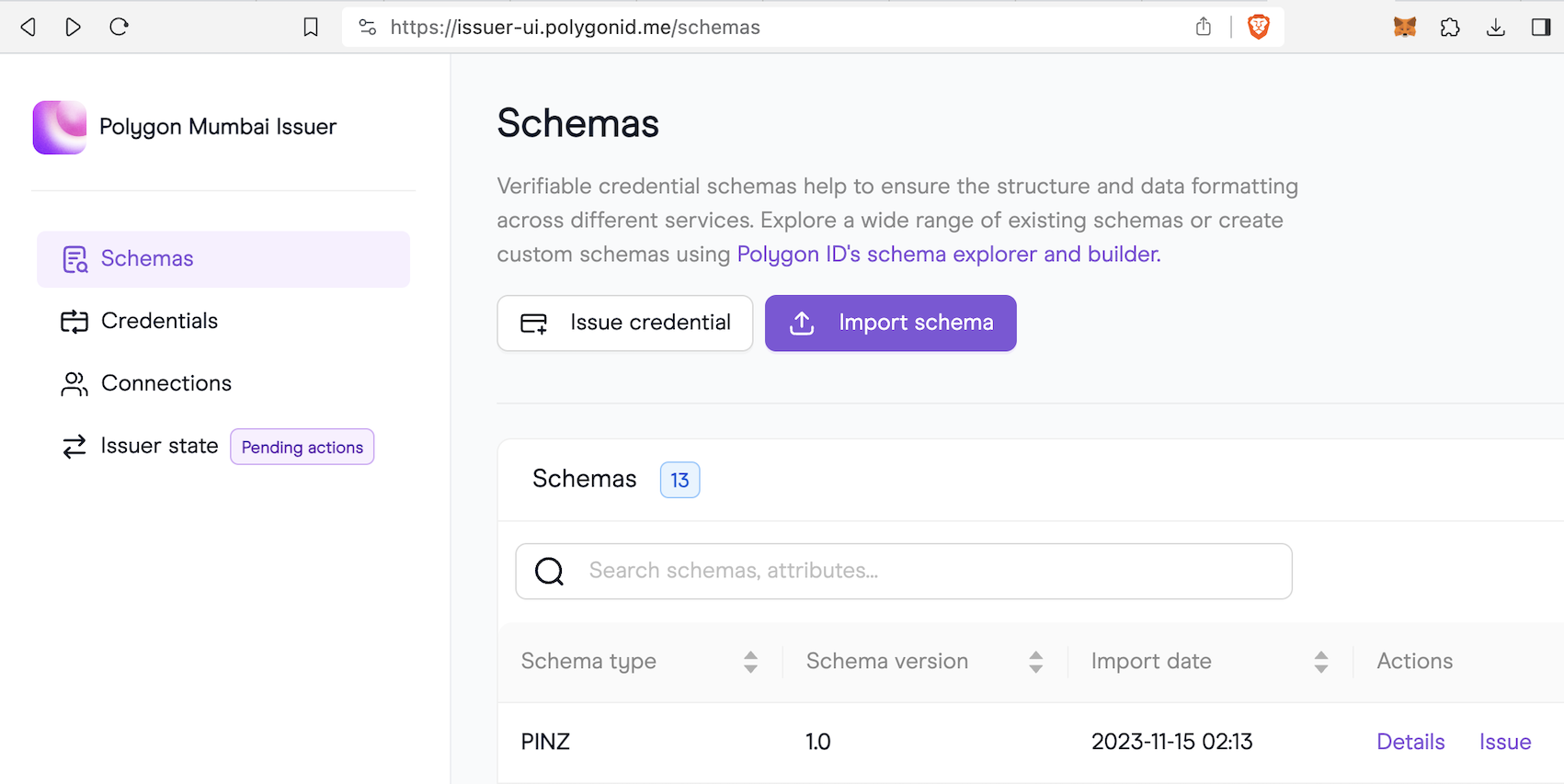
Issuer创建schema 进去后,我们准备颁发一个claim。首先创建一个schema,它表达了claim的格式,即claim应该存哪些字段,字段分别是什么数据类型。换言之,它是一个模板。我们创建一个简单的Schema。
Issuer创建Credentials 我们重点关心红色框内部的信息,id和type表示存储这两样信息,id表示字段的名称为role,type表示该字段存储在凭证的哪个插槽。这涉及到了claim的存储结构,我们后文会详细描述,大家只需要知道,claim可看作容量为8的数组,有8个插槽。有些插槽是存储特定信息的,例如claim的属主,claim遵循的格式、过期日期等元数据;有些则是为用户预留的,用户可以指定某个属性存储到哪个插槽中。
定义好claim后,我们来实例化一个具体的claim。此时我们还不知道接受者的did是多少,因此无法真正创建凭证。此时,我们创建的是一个Credentials,只有当后面holder来领取了这个Credentials,才会真正生成claim。这个Credentials里面填入了具体的字段,完成了Credentials的创建。
Holder领取Claim 如果说platform 是issuer的主场,那么polygon ID钱包就是holder的主场。holder打开polygon ID,先生成自己的did。然后,holder用pc打开issuer分发给他的链接,这个链接里面包含了一个二维码。
Holder创建Proof 好吧,polygon Id钱包目前不知道什么情况,至少笔者使用的版本没有找到构造proof的方法。不过笔者项目开发过程中,重新实现了整套polygon id,包括钱包,并自行实现了这套功能。
至此,本文已经演示完了polygon ID的基本用法,如果您想了解这其中幕后发生的事情,则接下来将开始介绍iden3的知识。
Round2: 概念 在我们先前对polygon ID的演示中,已经接触了Iden3的核心概念:schema,claims。现在来更详细的介绍一些基本知识。
密码学组件 在开始之前,先介绍一些iden3采用的基本密码学组件。这里不会介绍它们的具体实现和参数,具体内容我会在参考文档中给出。只会介绍它们的特性。
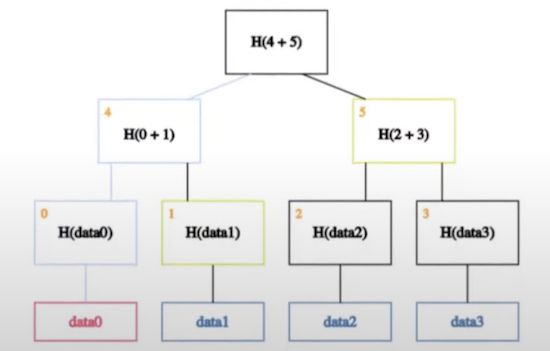
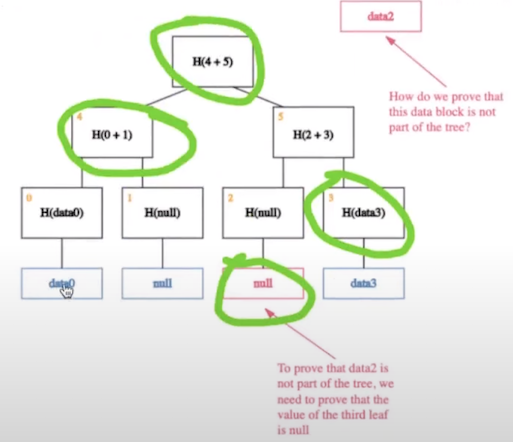
Sparse Merkle Tree 经典的merkle tree,被用来证明某样数据是存在的,只要Verifier能将Prover提供的证明(绿色部分)重新合成的根,和可信树根一致,就可以证明Prover真的持有对应叶子结点(红色部分):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 package mainimport ( "context" "fmt" "math/big" merkletree "github.com/iden3/go-merkletree-sql" "github.com/iden3/go-merkletree-sql/db/memory" ) func main () ctx := context.Background() store := memory.NewMemoryStorage() mt, _ := merkletree.NewMerkleTree(ctx, store, 32 ) index1 := big.NewInt(1 ) value1 := big.NewInt(10 ) mt.Add(ctx, index1, value1) index2 := big.NewInt(2 ) value2 := big.NewInt(15 ) mt.Add(ctx, index2, value2) proofExist, value, _ := mt.GenerateProof(ctx, index1, mt.Root()) fmt.Println("Proof of membership:" , proofExist.Existence) fmt.Println("Value corresponding to the queried index:" , value) proofNotExist, _, _ := mt.GenerateProof(ctx, big.NewInt(4 ), mt.Root()) fmt.Println("Proof of membership:" , proofNotExist.Existence) }
Sparse Merkle Tree的实现稍复杂一些,涉及到节点的动态更新等,细节读者可自行查阅资料。从模型上来讲,却很简单。Sparse Merkle Tree构建于“存储空间”之上。我们可以先想象出一个“存储空间”,每个存储单元对应一个递增编号。进程地址空间就是这样一个例子。接下来,相邻两个存储单元开始向上构建merkle tree,所得到的就是Sparse Merkle Tree。假如我想证明这个存储格子没有存储任何信息,那么先根据格子的编号找到存储内容,它的值为0;然后无脑构建merkle proof即可。也就是说,证明一个数据不存在,只要证明对应叶子结点值为0即可。
anyway,只需要记住:Sparse Merkle Tree可以证明数据不存在,在iden3中,claim的撤销、私钥更换、身份的撤销等神奇功能就依赖于这个技术。
BabyJubJub Key Iden3中,公私钥用于认证消息是否为对应did所发。Iden3采用了BabyJubJub曲线,而没有采用经典的secp256k1等曲线,因为BabyJubJub对zksnark很友好,这也是EIP-2494中推荐在circuits中使用的曲线,它的素数域是BN254的群阶。BabyJubJub曲线是SafeCurves工程的成果。该团队在设置了一组安全系数情况下,对BN254作为“主曲线”上进行派生,得到了的一条满足安全要求的曲线。另外,Zcash基于同样的原理(但是不同的p)构造了其他的JubJub曲线,也具有类似的效果。
就笔者个人经验来看,使用Babyjubjub体制的密码学,确实在构造电路方面节省的多,笔者在这次项目中尝试使用0xParc的ECDSA来构造一些基本的签名验证电路,约束多达数百k,跑个groth16的trusted setup都要几天几夜;相比之下,跑一个BabyJubjub体制下的电路,则2w约束不到。
为什么存在这样的差异呢,我们先要了解基础知识:
椭圆曲线本质是构建于素域Fp的加法循环群,点的加法离不开对p求模。例如扭曲爱德华曲线的点加法:
验证签名操作重度依赖于点加法,因此也就重度依赖于求模。
zksnark中,加法门、乘法门的操作,都是素域Fp上的带模操作,模为BN254曲线的阶(21888242871839275222246405745257275088548364400416034343698204186575808495617)
那么为什么babyjubjub造出来的电路约束这么少,比secp256k1少了整个量级,就是因为对求模的处理方式不同。如果我们想在zksnark做求模,有两种做法,一种自己在电路中实现求模,它会产生大量的电路约束。另一种是借助zksnark,不过仅限于模21888242871839275222246405745257275088548364400416034343698204186575808495617。如果你想对这个数取模,只需要正常做加法和乘法即可,求模操作是zksnark自带的,并不会产生额外的约束。
所以,产生约束数目的差异就很好解释了。secp256k1中,模p和zksnark自带的p是不一样的,那么只能自己在电路里生成模操作。但是babyjubjub的p,刚好和zksnark的p相同(它们都等于alt_bn128曲线的群阶),这就允许zksnark在处理bjj的求模操作时不必再去做取模操作,取模会在计算见证时自动完成 。这就好比你写solidity验签时,利用以太坊的预编译合约做验签名,肯定比用纯solidity实现验签要高效。如果我们查看babyjjubjub的代码,也可以印证这一点,它做的是扭曲爱德华曲线的点加法,但是无需任何求模:https://github.com/iden3/circomlib/blob/master/circuits/eddsa.circom BabyJubJub是众多明星项目心仪的曲线,对zk十分友好,也兼具安全性和效率即可 。如果想详细阅读相关资料,推荐阅读如下几篇材料:
https://z.cash/technology/jubjub/ https://eips.ethereum.org/EIPS/eip-2494#specificationhttps://github.com/iden3/iden3-docs/blob/master/source/docs/Baby-Jubjub.pdf
对Zk友好的哈希 在zksnark中,经常用到的哈希包括Poseidon Hash,Pederson Hash,MiMc Hash。它们都很常见,也出现在iden3的circomlib中,不过Poseidon Hash是Iden3项目主打的哈希方案。介绍它们的算法细节有点超出本文的内容了,也超出了我的能力。只粗浅的谈几点原理,权当茶余饭后的谈资:
Pederson 把域上的两个元素作为输入,结合椭圆曲线上的若干生成元,进行标量乘,得到的新曲线点的横坐标,这就是哈希的结果。换言之,记得公式公钥E = dG吧,Pederson Hash可看成这个公式的高配版。它的特点是同态性和隐私性。
PoseidonHash Poseidon Hash很容易和Pederson Hash搞混,尽管原理完全不同。它也是一种对ZK友好的哈希算法,并被Iden3中广泛的使用。提出于2020年。根据论文 和一些文章,它的约束数目要比Pederson Hash要节省8倍之多,对于PLONK还有据说40倍的提高。首先它基于海绵函数构造,在这个构造中,消息被分解为若干份,第一份消息和最左侧白色的状态的r部分进行异或, 所得结果和剩余的c部分一起进入函数f,生成新的状态,如此一轮一轮的操作,直到生成出结果。
初始化(Initialisation) :选择一组初始参数(如有限域、初始状态等)。多轮置换(Permutation) :使用特定的非线性函数(通常是“S-Box”,如乘方或立方)以及线性混合层对输入进行多次置换和混合。输出(Extraction) :在完成所有置换后,从最终状态中提取输出哈希值。
在Iden3中,大量的使用到了poseidon hash,无论是merkle tree,还是claim,还是身份状态。
Mimc Mimic也是一种面向zk设计的轻量级哈希,它只由加法和乘法构成,并且可以抵抗碰撞。它的结构上很简单,也是一轮一轮的处理,每一轮都根据输入i,密钥k,常数集合c来计算输出(即图中的➕):
MiMC 的一个典型数学表达式是基于有限域上的幂次运算。对于一个输入 x 和密钥 k,MiMC 哈希的一个简化版本可以表示为:
在这里:
x 是输入值。
k 是密钥。
e 是一个大的素数,用于幂次运算。
p 是一个大的素数,定义了运算所在的有限域。
\mod 表示模运算。
MiMC 之所以特别,是因为它的设计目标是在保持足够安全性的同时,最小化乘法运算的复杂度。
anyway,我们只要记住:iden3的circomlib实现了上述全部算法 ,甚至连变种也实现了;而且它们都是面向zk的哈希。而iden3本身则重度依赖poseidonHash。至于上述3个的特性如何,细节的原理是什么,哪个更安全,哪个更节省约束,为什么存在这种差异,超出了我的能力,请咨询群内大佬。
核心概念 现在开始,正式介绍Iden3的基本概念。如果理解了前面的内容,这部分会理解的很快。这一部分中,我们还是先不介绍具体的流程、动作是怎么实现的,而是先介绍幕后的东西,在文章结尾,会把本文的内容整合起来,彻底还原出整个系统是如何运作的。
Schema 格式前文已经介绍过,它定义了一个claim应遵守的格式,包括每个字段的名称,属性,存储插槽。此外,每个Schema还会生成哈希。
Claim 存储结构 Claim表示声明,上面记录了某did具有的属性有哪些。claim用中文应该叫声明,而不是凭证(credentials),这是两个不同的概念,声明代表数据,凭证代表证明。
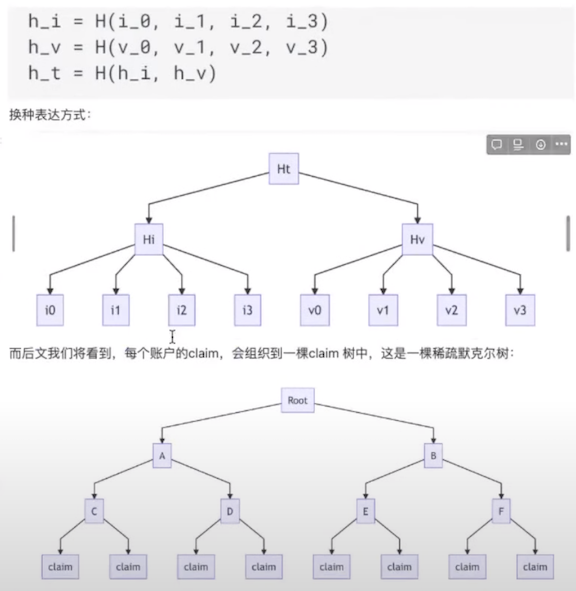
Claim由8个数据插槽构成,每个插槽包含了253位。前4个插槽,被称作“索引槽位”,原文IndexSlots,分别记为i0~i3。后4个插槽,被称作“值槽位”,原文ValueSlots。分别记为v0~v3。Claim的8个槽位,将按照下面的方式构建成merkle tree:尽量在索引槽位里面存储能够唯一化标记这个claim的数据 。例如,如果想做电子身份证,那么身份证号可以放在索引位,像住址等可以放在值槽位;另一方面,一定要避免两个Claim出现相同的Hi,不然发行、接受claim的时候,总是会报Sparse Merkle Tree的duplicate entry错误。这类似于,我们要存储[学生,班级]这个数据,那么应该以学生作为Hi,而不能以班级作为Hi,不然就会出现Hi的冲突。
下图是槽位布局的介绍 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 Claim structure Index: i_0: [ 128 bits ] claim schema [ 32 bits ] option flags [3] Subject: 000: A.1 Self 001: invalid 010: A.2.i OtherIden Index 011: A.2.v OtherIden Value 100: B.i Object Index 101: B.v Object Value [1] Expiration: bool [1] Updatable: bool [3] Merklized: data is merklized root is stored in the: 000: none 001: C.i Root Index (root located in i_2) 010: C.v Root Value (root located in v_2) [24 ] 0 [ 32 bits ] version (optional?) [ 61 bits ] 0 - reserved for future use i_1: [ 248 bits] identity (case b) (optional) [ 5 bits ] 0 i_2: [ 253 bits] 0 i_3: [ 253 bits] 0 Value: v_0: [ 64 bits ] revocation nonce [ 64 bits ] expiration date (optional) [ 125 bits] 0 - reserved v_1: [ 248 bits] identity (case c) (optional) [ 5 bits ] 0 v_2: [ 253 bits] 0 v_3: [ 253 bits] 0
i_0:存储元数据。包括如下信息:
claim schema:凭证schema的哈希,后面电路验证特定claim时,会去校验这个字段,例如对于记录公钥的auth claim,就要强行验证其等于”304427537360709784173770334266246861770”:
Subject:数据主体类型。如果留空,就表示发放给自己的,像auth claim(记录了公钥),就记录了issuer自己的公钥,自己发放给自己即可。如果这个值是010,就表示这个claim是描述其他did的,具体的did则存储在i_1槽位。如果是011,也表示这个claim是描述其他did的,但是did存储在i_0槽位。
version:版本号信息,对claim的更新操作需要用到。
Expiration、updatable等:略
i_1: 存储数据主体的did。(如果i0中Subjuject部分设为010)
i_2~i_3:留给用户使用。
v_0:存储元数据。包括如下信息:
revocation nonce:每个claim都具有一个独特的revocation nonce,是实现claim撤销的关键。
expiration date:claim过期日期。
v_1:储数据主体的did。(如果i0中Subject部分设为011)
v_2~v_3:留给用户使用。
这部分结构可能把大家绕晕了,那么换一种角度来理解它,就容易多了。假设我们是一所高校,现在我们要给学生颁发学生证,有效期为4年。假设此时已经是iden3的世界了,无论是学校还是学生,都有自己的did。那么典型地,凭证很可能长这样:
i_0的Subject部分设为010,表示这个claim是描述一个holder,而不是issuer自身
Expiration:设为true,因为4年就过期了。
i_1的identity部分,设为学生的did。
i_2~i_3:存放学校的名字,学生的其他信息等。注意,能用的空间很有限,只有i_2,i_3,v_2,v_3,请妥善使用空间。
v_0的expiration date:设为未来4年。
综上,我们已经在狭小的存储空间内,填上了“学生”“学校名字”“毕业年份”这几样关键信息。
也许读者会问,学校或单位颁发的证件,都会有一个盖章,对应到did中,不应该还有一个签名,或者issuer的did吗?如果没有这个信息,我作为验证者,我怎么知道你这个claim到底属于谁呢?请继续往下阅读,一步步揭开如何验证声明的有效性。
auth claim 在w3c did doc中,要求存储did的公钥。那么在iden3中,公钥会存储到auth claim中。auth claim是用户状态的一部分,最终会绑定到区块链上(即Issuer点击Publish issuer state时)。
Identity 从技术角度来看,一个身份包括三棵树:claims tree,revocation tree,roots of roots tree。
claims树 对于claims树而言,它包含了两类claim:自己作为issuer发给别人的claim,和作为holder所领取的claim。这是因为在Iden3的设计哲学中,身份包括两个基本的方面:我说出去的话,和别人对我说的话。这些claim均嵌入到claims树的叶子中。当zk verifier想要验证一个claim的有效性的时候,会验证claim存储在holder的claims tree中。
因此在开发的过程中,不管是holder还是issuer,都不得不去自己保存claim的原文。
revocation树 claim的撤销是个很常见的功能,例如学校可以开除学生,并把他的学生证无效化。笔者这次开发的项目中,也用到了撤销功能,有一个功能点就是我们自己复刻的增强版polygonID,会去访问knn3的数据源,一旦检测到holder在链上的数据已经不达标,则自动撤销。
现在请大家思考一个问题:作为一个issuer,给holder发放了一个claim,这个claim就流到了holder的手中,直觉上issuer就失去了对这个claim的控制权。那么issuer如何将其撤销呢?
答案就在revocation tree中。issuer的revocation tree也是一个Sparse Merkle Tree,它的叶子结点存放了被撤销的claim。如果一个issuer想撤销掉某已发放的claim,只需要取这个claim的revocation nonce,然后在revocation tree的revocation nonce插入这个claim的最新版本号即可(版本号涉及到更新过程,我们后面再来讨论)。revocation nonce也可以看成是claim的另一个id。
当verifier想要验证一个claim的有效性的时候,除了验证claim存储在holder的claims tree中以外,还要验证claim在issuer、holder中均未撤销。后面会详细介绍电路是如何验证的。
roots of roots树 claims tree每次添加完claims后,树根就会重新计算,新的树根也会被插入到roots of roots tree中。roots of tree的目的是使得claims的历史变更记录更容易被追踪。不过,就笔者目前看到的各类电路源码中,仅要求roots of roots提供的树根以用于合成identity state,而不会要求提供roots of roots相关的其他证明;也因此,笔者这次并没有维护roots of roots,直接保持空树,完全没有问题。
可见性 前面在介绍revocation tree的时候,提到了holder若要证明一个claim的有效性,除了提供存在性证明,还要提供issuer开具未撤销证明,这就要求issuer配合,如果issuer拒绝配合,holder就无法完成身份的验证。
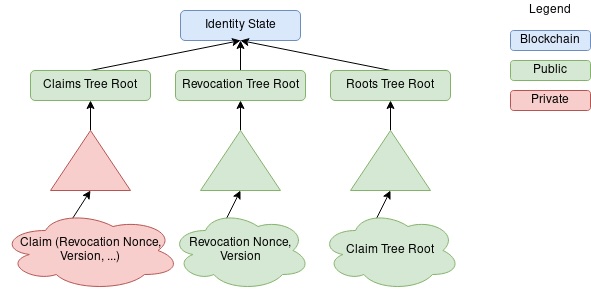
然而事实并非如此。这是因为,issuer的三棵树是有公有性规范的。下图中,红色部分表示私有—Issuer数据库;绿色部分表示公开存储,例如 IPFS;蓝色部分表示记录在区块链上。这样,由于revocation tree属于绿色部分,是公开存储的,因此holder直接从revocation tree开具证明即可,他只需用claim的revocation nonce,到revocation tree对应位置提供merkle proof,zk veritifer会验证这个proof,并结合其他两棵树的树根重新合成身份,并最终到链上去对比issuer的状态。
那么为什么claims tree要隐私存储呢?回顾claim的功能:它存储了的是属性,而did认为这些都是隐私数据。有些读者可能问,前面提到claim tree的叶子结点存的
又不是claim原文,而是claim的hValue部分,它也是个哈希呀?笔者对此的猜测是,这可能仍然存在撞库攻击的可能性,首先claim的schema是公开的,查到schema后,对对应的value字段暴力枚举所有可能性,还是有可能破解一些claim的内容的。因此,必须把claim叶子结点完全隐私化存储。
身份标识符 读者也许会好奇,前文演示polygonID时,用户有一个形如”11ruZLTyALHTYQz8tUx2zVa3EYXXBbgYEd7dmzXb3”,它是怎么生成的?
身份具有标识符,它表示身份的初始状态,由初始状态三棵树构成,该状态也被称为Genesis ID。初始情况下,revocation树、roots tree都是空的;而claim tree树包括了一个特殊的claim——authrization key,也称为auth claim,它保存了身份的公钥,后续所有的claim操作都必须提交和它公钥匹配的数字签名。身份标识符有31字节,由如下格式:
身份类型:占2字节,表示身份所遵循的标准。例如,例如哈希采用什么算法等等。
初始状态:占27字节,砍掉genesis state的前5个字节。
校验和:占2个字节。
这个31个字节,使用base58编码,就得到了did标识符。
Round3: 关键流程 介绍完基本概念,现在从用户角度出发,结合代码,梳理一下iden3中的一些关键流程的原理。
若要安装node的sdk:
若要安装go的sdk:
1 go get github.com/iden3/go-iden3-core
本文档采用go语言作为示例,由于iden3的sdk非常直观,所以即使您不熟悉golang,也可以很轻松看懂相关逻辑。
身份创建 创建身份的过程包括如下几步:
先创建一个随机的babyjubjub密钥对
将babyjubjub公钥嵌入auth claim
创建身份的三棵树
将auth claim嵌入到claims 树中
对三棵树执行hash,生成tree root,作为genesis state
根据genesis state构建did标识符。
至此,完成了身份的创建,iden3认为这个时候不必将身份记录到链上,后续状态发生变更,才需要把身份提交到链上。https://docs.iden3.io/getting-started/babyjubjub/
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 package mainimport ( "fmt" "github.com/iden3/go-iden3-core" "github.com/iden3/go-iden3-crypto/babyjub" "github.com/iden3/go-merkletree-sql/v2" "github.com/iden3/go-merkletree-sql/v2/db/memory" "github.com/iden3/go-iden3-crypto/poseidon" ) func main () babyJubjubPrivKey := babyjub.NewRandPrivKey() babyJubjubPubKey := babyJubjubPrivKey.Public() authSchemaHash, _ := core.NewSchemaHashFromHex("ca938857241db9451ea329256b9c06e5" ) revNonce := uint64 (1 ) authClaim, _ := core.NewClaim(authSchemaHash, core.WithIndexDataInts(babyJubjubPubKey.X, babyJubjubPubKey.Y), core.WithRevocationNonce(revNonce)) authClaimToMarshal, _ := json.Marshal(authClaim) fmt.Println(string (authClaimToMarshal)) ctx := context.Background() clt, _ := merkletree.NewMerkleTree(ctx, memory.NewMemoryStorage(), 40 ) ret, _ := merkletree.NewMerkleTree(ctx, memory.NewMemoryStorage(), 40 ) rot, _ := merkletree.NewMerkleTree(ctx, memory.NewMemoryStorage(), 40 ) authClaim := core.NewClaim(core.AuthSchemaHash, core.WithIndexDataInts(X, Y), core.WithRevocationNonce(0 )) hIndex, hValue, _ := authClaim.HiHv() hIndex clt.Add(ctx, hIndex, hValue) fmt.Println(clt.Root().BigInt(), ret.Root().BigInt(), rot.Root().BigInt()) hi, hv, _ := newClaim.HiHv() clt.Add(ctx, hi, hv) authMTPProof, _, _ := clt.GenerateProof(ctx, hIndex, clt.Root()) authNonRevMTPProof, _, _ := ret.GenerateProof(ctx, new (big.Int).SetUint64(revNonce), ret.Root()) genesisTreeState := circuits.TreeState{ State: state, ClaimsRoot: clt.Root(), RevocationRoot: ret.Root(), RootOfRoots: rot.Root(), } }
添加claim 添加claim的过程包括:
撤销claim 撤销claim的步骤如下:
更新claim 回顾claim的结构,如果claim的i_0中开启了updatable功能,那么就允许版本更新;版本号嵌入到i_0插槽中,意味着版本变了,那么hIndex也就变了,在claim tree中的存储位置也变了。
更新claim的逻辑,就是把旧版本撤销掉,然后构建一个新的claim,然后把新的版本号更新revocation tree中。具体步骤:
取旧的claim的revocation nonce,并将它当前版本号插入到revocation tree的value部分中。
创建新的claim,它的版本号要比先前的更高。新的claim会插入到claim tree。
构造zk证明:状态转移证明 (证明的原理,后文统一解释)
将zk证明同步到state合约(记录did的所有states),state合约验证zk proof和公开输入后,将该账户新的状态存储到合约内部。
假设最新的claim版本号是n,如果我们试图基于一个旧的claim(其版本号为v,v < n)构造有效性证明,会怎么样呢,理应是验证失败,因为验证版本的逻辑丽颖是,如果claim是updatable,则要求用户提交rev tree中的证明(即最新版本n的逻辑),然后取claim中的version进行对比,即验证version == v;反之如果是不updatable的,则只需提供叶子为(revocation nonce, 0)的证明即可。但是我源码中并没有看到这段版本验证逻辑,甚至都没有看到提取version字段校验的逻辑,所以Iden3究竟能不能支持更新,还请各位读者继续深入研究,这个场景我自己也没有实际验证过。
私钥更换 文档中私钥替换被称为key rotation。用户只需要把旧的私钥对应的auth claim撤销,再把新的auth claim存入到claim tree,随后同步状态即可。步骤:
旧的auth claim插入到revocation tree中
新的auth claim插入到claim tree中
计算新的状态根
构造zk证明:状态转移证明 (证明的原理,后文统一解释)
将zk证明同步到state合约(记录did的所有states),state合约验证zk proof和公开输入后,将该账户新的状态存储到合约内部。
账户注销 如果用户想注销自己的身份,只需将自己的所有的auth claim全部撤销,等于自己的所有公钥都被宣布为无效。这样新的状态根一旦上链,若拿着以前的公钥构造的证明,那么要么zk这里identity state对不上,要么验证公有输入的时候和合约对不上,验证不可能通过。(注:State合约中保存的是identity历史的所有state,一般情况下是用公开输入的identity state和最新的合约中state对比;但如果提交的state能和先前某一个state对的上,那么文档中的说法是“由应用自行决定如何处理”)
具体:
将所有的auth claim插入到revocation tree
计算新的状态根
构造zk证明:状态转移证明 (证明的原理,后文统一解释)
将zk证明同步到state合约(记录did的所有states),state合约验证zk proof和公开输入后,将该账户新的状态存储到合约内部。
身份认证 先回顾一下最传统的登陆流程。
第一种,用户提交用户名和密码,服务端把密码加盐哈希,然后和数据库里保存的哈希值做对比。
第二种,第三方登录,包括授权码、PKCE、凭证式等模式;以授权码模式为例,若要登陆应用网站,可以先去其他身份服务网站登陆,然后拿到授权码,再像应用网站提交授权码,应用网站向认证网站换取accessToken,然后使用token向身份网站请求后续用户数据……
而现在基于did和zk技术,iden3提出了一种新的身份登陆协议。这种协议更像是用户名、密码登录的增强版本,这里面的“用户名”是就是用户的did,“密码”则是zk身份证明。协议包括两个角色:用户和应用。用户向应用请求身份认证,认证后如常规web2一样拿到token。具体步骤:
至于这里面“authentication电路”的约束逻辑,我们后文解释。
这个技术在polygonID中是,被应用于领取claim:当issuer发放完offer的时候,holder用polygon钱包扫码,扫出来的就是认证json。holder钱包构造好证明后,将自己的did连同身份提交回platform网站,身份认证通过后,platform构造claim,包括将claim的subject部分设为holder did。然后把这个claim返回给holder钱包,holder钱包存下该claim,并后面按时同步给链上state合约。
提供凭证 还是那个经典问题:你如何在不暴露年龄的情况下,证明自己大于18岁?通常是构建一个电路,用户提供两个输入:出生年月(私有输入)和当前日期(公有输入)。zk电路验证当前日期减去出生年月 大于 18;而对于验证者,除了校验zk,还要验证公开输入,即校验当前日期确实等于当前日期。电路类似如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 template AgeOver18() { signal input birthYear; signal input currentYear; signal output age; age <== currentYear - birthYear; assert(age >= 18 ); } component main = AgeOver18();
诸如此类,都是常见的需求。为了能够让用户能够避免每次都写这样的代码,Iden3将比较常见的查询需求都统一起来,构建了一套ZKL(Zero Knowledge Language)。用户将操作符、输入、操作数据作为输入,其中数据输入是私有的,其余公开的。提供 它包括日常的功能:
Equal:相等比较。
Less Than:小于
Greater Than:大于
In:属于某个集合。例如角色 in [‘Boss’, ‘Manager’, ‘Employee’]这种。注意不是范围证明。
Not In:不属于某个集合。
好吧,并没有实现范围证明,希望将来可以实现。
Round4: 源码导读 理解了上述大部分逻辑,阅读源码就很轻松了。这里主要列一下State合约,还有几个重要电路。理解了这些代码,基本等于掌握了Iden3的核心逻辑。
State合约 State合约见:https://github.com/iden3/contracts/blob/master/contracts/state/State.sol
核心函数transitionState
authentication电路 代码:https://github.com/iden3/circuits/blob/master/circuits/lib/authentication.circom
authentication用于证明用户持有一个有效的公钥。公钥记录在auth claim中。验证逻辑:
authclaim属于holder的claims树
authClaim未被holder撤销(即revocation tree可以提供缺失证明)
holder状态等于三棵树的哈希
签名必须能用authclaim里的公钥验证
除了authentiction,还有一个authenticationWithRelay,它用于某个relayer帮助Provoder转交证明的情况。验证逻辑:
authclaim属于holder的claims树
authClaim未被holder撤销(即revocationtree可以提供缺失证明)
holder状态等于三棵树的哈希
签名必须能用authclaim里的公钥验证
relayer要提供一个relay claim,里面的数据主体是holder
relayer的relay claim必须在relayer的claims树中存在
relayer状态等于三棵树的哈希
stateTransition电路 代码:https://github.com/iden3/circuits/blob/master/circuits/lib/stateTransition.circom
如果旧状态是genesis状态,则用户id是否和genesis对的上
sanity check:新状态不为0、新状态不等于旧状态
验证auth claim的有效性,包括它的存在性证明、未撤销证明(还原的树根需和输入旧状态)
根据auth claim的公钥,验证签名的有效性,其中消息摘要为新旧状态拼起来的poseidon哈希
crerdentialAtomicQueryMPT电路 该电路用于基于claim数据,进行选择性披露:https://github.com/iden3/circuits/blob/master/circuits/lib/query/credentialAtomicQueryMTP.circom
它的逻辑很简单,就是检查claim的有效性,然后检查query的有效性。
Round5: 回顾应用 我们已经介绍完了Iden3的核心内容。为了加深印象,现在我们回到polygonID,重新梳理一遍整个流程。
注册issuer 用户注册后,后台实际是调用前文“身份创建”的逻辑,即创建babyjubjub密钥、添加auth claim、计算genesis state、计算did。
Issuer创建schema 这里面,issuer构建了一个schema,这是一个jsonld文件,存储在了数据库。
Issuer创建Offer 这里面,issuer创建了一个offer,然后存入数据库。
Holder领取Claim holder点开offer link,此时页面会向后台请求auth json,即前文“身份认证”过程。holder钱包扫码这个二维码。
Platform若想可信地获取到钱包的二维码,需要先生成一个json.
它规定了手机端应该提供何种方式来证明自己的身份,zk?签名?如果用zk,使用哪个电路?等等。以这个json为例,它要求使用auth电路来证明身份,auth电路则本质是验证用户的签名,而challenge则是待签署的数据。
这个json可以使用二维码,邮箱等方式发送给手机钱包。手机钱包拿到这个json后,需要进行如下步骤处理:
polygon platform在收到响应后,执行如下验证过程:
在笔者开发中,我们对这部分做了小小的扩展。我们的业务场景是,用户还要额外提供自己的polygon钱包地址和签名,platform还要额外验证该钱包。验证后,platform会向knn3的地址(例如https://credentials.knn3.xyz/nft/0x64e16D972Dac15d0700764f64C9011432d59A79C)
获取链上的数据,如果和预设条件一致,则增发claim。这里面,zk证明和钱包证明必须结合起来,必然攻击者把钱包替换掉。笔者最开始尝试使用0xParc的ECDSA纳入到authentication电路里,但是这样生成了100k的约束,光跑groth16的可信设置,一天一夜都没跑完。后面换了个简单的做法,在zk proof公有输入中,babyjubjub的签名使用的那个哈希,也加入钱包的内容,这样platform验证时,先通过钱包签名恢复出polygon地址,然后计算哈希,哈希必须和zk公有输入一致,然后验证zk proof。这样就解决了上述安全性问题,且约束仅有2.5w。
Holder创建Proof holder根据claim,使用前文zkl构建对claim的选择性披露,如果claim的数据达到一定条件,就让另一个SBT合约给他签发一个徽章。
这里面,回忆一下,若要证明claim的有效性,必须提供issue的revocation tree未撤销证明。这里面笔者因为时间很赶,直接让platform开了一个接口去提供这个证明。实际上,revocation tree应该存储在IPFS或者AR上。
Round6:实战踩坑 iden3本身还在迭代,开发过程中,会遇到不少问题。记录一下踩到的坑,让诸位避免重复踩坑。
问题1: 我应该使用哪些sdk? iden3的sdk比较杂乱,约有数十个仓库,有些代码都是几年前的,而且文档几乎是没有;甚至还有很多代码里很有注释掉的代码。经过摸索,笔者最终选择了这些仓库:
1)iden3核心: go-iden3-core
https://github.com/iden3/go-iden3-core https://github.com/0xPolygonID/tutorial-examples/tree/main/issuer-protocol
2)merkle tree: go-merkletree-sql
https://github.com/iden3/go-merkletree-sql/tree/master/db/memory
3)电路输入创建: go-circuits
https://github.com/iden3/go-circuits
4) 见证计算:go-circom-witnesscalc
https://github.com/iden3/go-circom-witnesscalc
5) 证明生成&&验证: go-rapidsnark
https://github.com/iden3/go-rapidsnark
问题2: 如何为账户构建merkle tree持久化存储? 首先,merkle tree支持postgre存储。它的表结构如下(https://github.com/iden3/go-merkletree-sql/blob/master/db/pgx/schema.sql ):
如果我们阅读https://github.com/iden3/go-merkletree-sql/blob/master/db/pgx/sql.go,但这基本就是一层壳,若真要使用postgresql,我们还是需要自己实现一个DB的实现类,来支持上述查询。
问题3:计算见证时报reference等错误? 注意,截止目前,go-circom-witnesscalc最新发布的版本是1.0.2版本有bug,跑最基本的电路都会报各种wasm自身的错误。经过研究,这是因为witness_calculator文件在1.0.2版本之前存在bug。(https://github.com/iden3/go-circom-witnesscalc/blob/master/circom2witnesscalc.go )存在bug,不过已在master分支解决,待发布。我自己的解决办法是直接拷贝witness_calculator的master分支代码到本地,用这份来代码来执行计算见证即可。
额外吐槽一下,Iden3有些细节做的确实不太好,比如circom教程中,按照文档复制粘贴过来的基础电路竟然跑不通:https://github.com/iden3/snarkjs/issues/252
问题4: 对go-rapidsnarkjs环境相关问题? 因为使用了c库,因此底层环境要选择正确。需要参考操作系统和cpu架构是否支持(在https://github.com/iden3/go-rapidsnark/tree/main/prover)。
在开发过程中,笔者采用macos 12 + m1,没有遇到任何问题。但在部署时,部署到centos7服务器时,遇到了问题,需要选择合适的gcc版本。用centos自带的4.8无法完成编译;但用最新的10+版本又无法安装所要求的glibc 2.18。所以在朋友的帮助下,最终搞定了环境。最后选择的gcc是v7。
问题5: 见证计算经常报验证失败,如何debug?最常遇到了什么样的bug? 计算见证时,除了计算各种信号,还会检查信号约束是否满足条件。如果遇到bug,怎么解决呢?
这种错误源于电路输入中某个字段不正确。为了找出这个字段,笔者的做法很简单,首先,项目中要打印出用go-circuits构建的zk 输入;然后,zk电路中可以在关键节点中用log语句打印输入的值;然后把这个输入拷贝到input.ajson中,手动运行电路,然后看看是哪里报错。基本就可以推断出代码中是哪一步错误了,然后继续对代码中关键部分打日志、调查。很快就能找到错误原因。
以笔者的经验,遇到过genesis state和id不一致,也就是stateTransition的这一步,原因来讲,我自己遇到的有两种:
1)编码错误,树根传错了(我曾经传了两个claimtree + roots of roots tree计算树根),导致genesisState计算错误,自然和id对不上;
Round7: 要点回顾 本文中,介绍了iden3的应用、原理、源码。现在来回顾一下全文的要点。
在iden3中,实现了“issuer给holder发claim,holder选择性地披露claim的一些性质给verifier”这样一个标注你的did故事;
每一个身份都有三棵树构成,claims树包括发行或者接收的claim;revocation tree包含被撤销的claim;roots of root tree记录每次claims树根的变动。三棵树均采用SMT,SMT用于提供不存在性的证明,这对revocation tree很重要,可用于提供未撤销证明。三棵树的树根拼起来的哈希,就构成了身份的当前状态,该状态不定时地同步到链上。身份初始情况下都包含一个auth claim,它包含了babyjubjub公钥。而初始情况下的身份状态,决定了它的id。
每个claim有8个插槽,其中4个是索引槽,4个是值槽。索引槽位决定了claim在claims tree中的位置;claim中既包括“数据主体”“过期时间”这样的元数据信息,又允许用户自己填写所需数据。数据的格式被称为schema,这是一个jsonld文件,它的哈希值也被嵌入到schema中。
iden3支持claim的发行、撤销等能力。每当发行或接受一个claim时,它被私有地存放到claims树中;而若撤销时,revocation tree将公开地将对应revocaiton nonce位置标记上这个claim。
当要证明身份或者提供proof时,prover通常要除了提供自己claim在claims树中的证明,还要提供在自己这里的未撤销证明,还有在issuer那里的未撤销证明。这也意味着,issuer有权力撤销自己发放的claim。证明以zk的形式进行,验证者需要验证zk本身数据的自洽性,典型地包括使用auth claim验证签名,还有输入的用户状态根和三棵树恢复出的状态根一致;此外还要验证公开输入的有效性,例如校验用户状态根和链上记录的一致。
如果要披露一个claim的属性,除了提供上述claim本身的有效性证明,还可通过ZKL形式,提供相关的操作符和输入,包括等于、大于、小于、IN、NOT IN这几种常见的操作,真正实现了选择性披露。
最后,Iden3还基于这些基础构件,提出了一套基于Iden3的身份认证协议,Prover通过Verifier所要求的认证方式调用Verifier的回调发送zk proof,以提供对自己did的证明,在认证通过后可以获取token,或者像polygonID那样,将Provder的did嵌入claim、并发放claim。
参考资料 官方文档:https://docs.iden3.io/protocol/spec/#properties
代码仓库:https://github.com/iden3
polygonID:https://issuer-ui.polygonid.me/
其他文档:https://eprint.iacr.org/2019/458.pdf https://medium.com/zokrates/efficient-ecc-in-zksnarks-using-zokrates-bd9ae37b8186 https://z.cash/technology/jubjub/ https://eips.ethereum.org/EIPS/eip-2494#specificationhttps://github.com/iden3/iden3-docs/blob/master/source/docs/Baby-Jubjub.pdf