FMR-市场风险

按照风险的驱动因素，金融风险可以分为市场风险market risk，信用风险credit risk，操作风险operational risk，流动性风险liquidity risk。

最常见的市场风险包括利率风险，汇率风险，通货膨胀风险，证券价格风险，波动率风险等。

市场风险分析方法：

1. 缺口分析法 gap analysis，即资产负债缺口分析法。当利率发生变化时，资产和负债之间产生“缺口”，通过比较缺口的大小，可以得到利率变化时市场价值变动的程度，亦即产生的利率风险的大小。GAP（缺口）= RSA（利率敏感性资产）- RSL（利率敏感性负债）

2. 久期分析法 duration analysis，即持续期分析法或者期限弹性分析法。其通过对各时间段段缺口赋予相应权重，得到加权缺口，然后对这些加权缺口求和，以此估算利率变动对市场价值的影响。

相对于缺口分析只是考虑净收入的变化，久期分析则考察资产或者负债的价值，是一种更为准确的利率风险计量方法。

3. 场景分析法 scenario analysis，又称假设分析法 what-if analysis。通过设定不同的情景，分析在每一种情景下的收益或者亏损，从而对整个投资组合的未来风险情况进行评估，做出最佳决策。
4. 投资组合理论 portfolio theory，是一种衡量市场风险的方法。
5. 希腊字母估计市场风险。

希腊字母	符号	风险评估
Delta	Δ	标的资产价格变化引起金融衍生品价格变化
Gamma	Γ	标的资产价格变化引起Delta变化
Theta	Θ	时间引起衍生品价格变化
Vega	Λ	市场波动率变化引起金融衍生品价格变化
Rho	ρ	利率变化引起金融衍生品价格变化

6. 风险价值 Value at Risk - VaR，也叫在险价值。作为经典的市场风险度量，可以用来评估资产的风险，帮助金融机构合理分散或者规避风险。摩根大通J.P.Morgan Chase开源了RiskMetrics系统，很快被金融机构采用，广泛地用来计算包括市场风险、信用风险以及操作风险等在内的金融风险。

   6.1 参数法计算风险价值 parametric approach，一般假设未来收益满足正态分布，这是因为如股票收益率等风险因子一般都可以用正态分布近似，而资产组合通常也可以用风险因子等线性组合来表示，并且正态分布的任意线性组合仍然为正态分布，因此资产祝贺的预期收益分布仍然为正态分布。

   在市场上，价格低标准差通常变化较大，价格本身对于标准差来说，变化并不大。所以，参数法的关键是要计算出分布的标准差σ，正因为如此，参数法又时也被称为方差协方差方法。该原理容易理解，计算量也较小。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pandas_datareader
import scipy.stats as stats
from mpl_toolkits import mplot3d
from matplotlib import cm

# 假设投资组合包含以下公司
tickers = ['GOOGL','FB','AAPL','NFLX','AMZN']
ticker_num = len(tickers)
price_data = []
for ticker in range(ticker_num):
    # 获取股票的历史数据
    prices = pandas_datareader.DataReader(tickers[ticker], start='2015-11-30', end = '2020-11-30', data_source='yahoo')   
    price_data.append(prices[['Adj Close']])
    df_stocks = pd.concat(price_data, axis=1)
    
# stock log returns计算“日对数回报率”
logreturns = np.log(df_stocks/df_stocks.shift(1))[1:]  
logreturns.columns = tickers 
logreturns.head() 

# 假设它们的对数回报率满足正态分布，下面代码计算并展示股票的回报率分布
# plot log return distribution for GOOGL
plt.style.use('ggplot')
mu, std = stats.norm.fit(logreturns['GOOGL'])
x = np.linspace(mu-5*std, mu+5*std, 500)
logreturns['GOOGL'].hist(bins=60, density=True, histtype="stepfilled", alpha=0.5)
x = np.linspace(mu - 3*std, mu+3*std, 500)
plt.plot(x, stats.norm.pdf(x, mu, std))
plt.title("Log return distribution for GOOGL")
plt.xlabel("Return")
plt.ylabel("Density")

# plot log return distribution
rows = 2
cols = 2
fig, axs = plt.subplots(rows, cols, figsize=(12,6))
ticker_n = 1
for i in range(rows):
    for j in range(cols):
        mu, std = stats.norm.fit(logreturns[tickers[ticker_n]])
        x = np.linspace(mu-5*std, mu+5*std, 500)
        axs[i,j].hist(logreturns[tickers[ticker_n]], bins=60, density=True, histtype="stepfilled", alpha=0.5)
        axs[i,j].plot(x, stats.norm.pdf(x, mu, std))
        axs[i,j].set_title("Log return distribution for "+tickers[ticker_n])
        axs[i,j].set_xlabel("Return")
        axs[i,j].set_ylabel("Density")
        ticker_n = ticker_n + 1
plt.tight_layout()

​ 6.2 历史法计算风险价值 historical approach，这是一种全值估计方法 full revaluation，具体是指利用风险因子的历史数据，计算过去某段时期收益的频度分布，并以此来模拟风险因子的未来收益分布，然后根据置信水平，确定相应的最大可能损失。

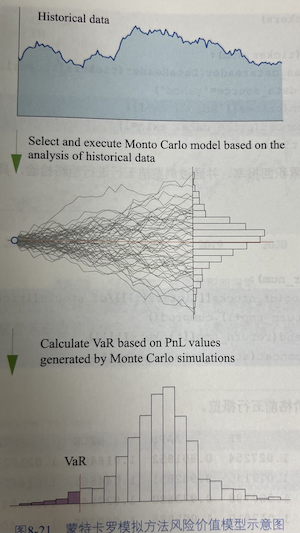
​ 6.3 蒙特卡洛法计算风险价值 Monte Carlo simulation，这也是风险价值计算中最常应用的模型之一。首先通过分析历史数据建立风险因子的随机过程模型，然后反复模拟风险因子变量的随机过程，每一次模拟都可以得到风险因子的一个未来变化的情景，以及投资组合在持有期期末的一个可能价值。通过大量的模拟，投资组合价值的模拟分布将最终收敛于该组合的真实分布，根据该分布，可以计算风险价值。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pandas_datareader
import seaborn as sns

# 假设投资组合包含以下公司
tickers = ['GOOGL','FB','AAPL','NFLX','AMZN']
ticker_num = len(tickers)
price_data = []
for ticker in range(ticker_num):   
    prices = pandas_datareader.DataReader(tickers[ticker], start='2015-11-30', end = '2020-11-30', data_source='yahoo')   
    price_data.append(prices[['Adj Close']])
    df_stocks = pd.concat(price_data, axis=1)
df_stocks.columns = tickers

# 然后计算股票的累积回报率
# cumulative returns
stock_return = []
for i in range(ticker_num):  
    return_tmp = np.log(df_stocks[[tickers[i]]]/df_stocks[[tickers[i]]].shift(1))[1:]  
    return_tmp = (return_tmp+1).cumprod()
    stock_return.append(return_tmp[[tickers[i]]])
    return_all = pd.concat(stock_return,axis=1)
return_all.head()

# 利用曲线更直观地展示所有股票的回报率
# plot cumulative returns of all stocks
plt.style.use('ggplot')
for i, col in enumerate(return_all.columns):
    return_all[col].plot()
plt.title('Cumulative returns')
plt.xlabel('Date')
plt.ylabel('Return')
plt.xticks(rotation=30)
plt.legend(return_all.columns)

# 设定投资组合中各个股票的比重，并且在持有期内保持不变。进而计算得到整个投资组合的预期回报和股价
# lastest return and price values
latest_return = return_all.iloc[-1,:]
latest_price = df_stocks.iloc[-1,:]
sigma = latest_return.std()
# weights for stocks in the portfolio
stock_weight = [0.2, 0.3, 0.1, 0.15, 0.25] 
# calculate expected return
expected_return = latest_return.dot(stock_weight)
print('The weighted expected portfolio return: %.2f' % expected_return)
# calculate weighted price
price = latest_price.dot(stock_weight)
print('The weighted price of the portfolio: %.0f' % price)

#假设该投资组合的回报率符合正态分布，以一天中的每一分钟作为步长，即分为1440个节点，利用蒙特卡洛模拟随机产生500个回报率数值。
# monte carlo simulation
MC_num = 500
confidence_level = 0.95
time_step = 1440
for i in range(MC_num):  
  daily_returns = np.random.normal(expected_return/time_step, sigma/np.sqrt(time_step), time_step)
  plt.plot(daily_returns)
plt.axhline(np.percentile(daily_returns,(1.0-confidence_level)*100), color='r', linestyle='dashed')
plt.axhline(np.percentile(daily_returns,confidence_level*100), color='g', linestyle='dashed')
plt.axhline(np.mean(daily_returns), color='b', linestyle='solid')
plt.xlabel('Time')
plt.ylabel('Return')
# 可视化，红线处为风险价值
# plot return distribution
sns.distplot(daily_returns, kde=True, color='lightblue')
plt.axvline(np.percentile(daily_returns,(1.0-confidence_level)*100), color='red', linestyle='dashed', linewidth=2)
plt.title("Return distribution")
plt.xlabel('Return')
plt.ylabel('Frequency')
plt.show()

# 假设初始投资金额为100万美元，得到VaR值为 33185
initial_investment  = 1000000
VaR = initial_investment*np.percentile(daily_returns,(1.0-confidence_level)*100)
print('The value at risk is %.0f' % VaR)

若为了获得更多的场景，更多的模拟，这里的计算量会迅速上升，从而导致整体的运算速度较慢。

关联阅读 - FMR-波动率