FMR-波动率

Posted on Edited on

金融资产价格包括股票，期货，期权，目前本人在思考加密货币的价格是否可以套用经典的金融风险模型，学习笔记汇报如下，由于比较书写数学公式不便，本文只记录了关键说明和程序代码。

1. EWMA

指数移动加权平均 - Exponentially Weighted Moving Average, EWMA.

EWMA波动率迭代告诉我们，当前一天的波动率是前一天波动率的函数，这也提供了一种用过去波动率预测未来波动率的方法。这种方法，不需要保存过去所有的数值，而且计算量较小，因此在实际中广泛使用。

The ewm() function is used to provide exponential weighted functions. 指数加权功能。

1
2
3
4
5
6
7
8
9
10
import pandas as pd

# Creating the series. Using the range() function, we create a series and set the index to shot.
my_series=pd.Series(range(1,20,5), index=[x for x in 'shot'])

# Printing the series
print(my_series)

# Using Series.ewm(). We calculate the exponential weight of elements in the series using the ewm() function and set the com and adjust parameters.
print(my_series.ewm(com=0.5, adjust=True).mean())

其中，

1
Series.ewm(self, com=None, span=None, halflife=None, alpha=None, min_periods=0, adjust=True, ignore_na=False, axis=0)

  • com: This represents the decay in terms of the center of mass, α=1/(1+com), for com≥0. 根据Center of Mass质心指定衰减。

  • span: This represents the decay in terms of the span, α=2/(span+1), for span≥1. 根据跨度范围（例如，天数）指定衰减。

  • halflife: This represents the decay in terms of the half-life, α=1−exp(log(0.5)/halflife), for halflife>0. 根据半衰期指定衰减。

  • alpha: This indicates smoothing factor α, 0<α≤1. 衰减系数。

  • min_periods: This represents the minimum number of observations needed to have a value in the window. The default value is 0.

  • adjust: This is divided by the decaying adjustment factor into the initial periods to consider the imbalance in the relative weightings (looking at the EWMA as a moving average). 计算权重的方式。

  • ignore_na: This specifies that the missing values should be ignored when calculating weights. The default is False. 如何对待空值。

  • axis: The default value is 0. It specifies the axis on which the function is to be performed. If the value is 0, the operation is performed across the rows. Otherwise, the operation is performed across the columns. 数轴。

2. 自回归条件异方差模型ARCH

EWMA与实际情况有不符合的地方，例如，股票收益的波动率是随着时间而变化的。异方差（heteroscedasticity）是指一系列的随机变量值的方差不同。这个模型以自回归方式，通过刻画随时间变异的条件方差，成功解决了时间序列的波动性问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np
import pandas_datareader
import matplotlib.pyplot as plt 
from arch import arch_model
# sp500 price
sp500 = pandas_datareader.data.DataReader(['sp500'], data_source='fred', start='12-28-2009', end='12-28-2020')
# daily log return
log_return_daily = np.log(sp500 / sp500.shift(1))
log_return_daily.dropna(inplace=True)
# ARCH(1) model
arch=arch_model(y=log_return_daily,mean='Constant',lags=0,vol='ARCH',p=1,o=0,q=0,dist='normal')
archmodel=arch.fit()
archmodel.summary()
archmodel.plot()

3. 广义自回归条件异方差模型GARCH

GARCH是对ARCH建模的一种重要推广。其后，又有诸如NGARCH，IGARCH，EGARCH等一系列针对不同应用等衍生模型相继出现。

1
2
3
4
5
# GARCH(1,1) model
garch=arch_model(y=log_return_daily,mean='Constant',lags=0,vol='GARCH',p=1,o=0,q=1,dist='normal')
garchmodel=garch.fit()
garchmodel.summary()
garchmodel.plot()

4.模型比较

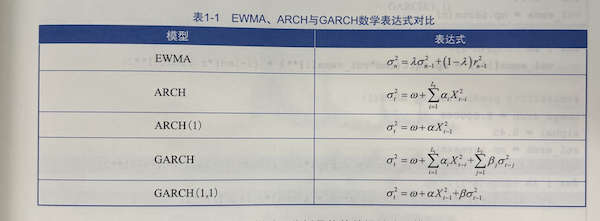
对于EWMA模型，利用了通常用的0.94，即 JP Morgan 的RiskMetrics采用的设定。所以，下图中，EWMA中的 λ 通常为 0.94。当GARCH(1, 1)模型的参数 β=0 时，即为ARCH(1, 1)模型。而当 ω=0，α=1-λ，β=λ 时，GARCH(1, 1)模型变换成为EWMA模型。

5.隐含波动率

请参考相关阅读中的金融分享管理 - 视频 https://space.bilibili.com/513194466/channel/seriesdetail?sid=650176。

疑问：市场波动率模型以布朗运动位基础，这真的符合市场的实际情况吗？特别是长期投资？如乔布斯，国家资本主义，等等。

相关阅读：