椭圆曲线密码
定义
椭圆曲线和很多学习完基础代数之后见过的方程差不多。y在等号的左边,而x在等号的右边。椭圆曲线有如下的形式:
$$
y^2 = x^3+ax+b
$$
你肯定接触过其他类似的方程。比如,在基础代数课上就学过线性函数:
$$
y=mx+b
$$
你可能还记得m叫作斜率,b叫作截距。你也能画出线性函数图像。类似地,你可能也熟悉二次函数和它的图像:
$$
y=ax^2+bx+c
$$
在学习代数时,你还接触过更高阶的函数比如三次函数及其图像。
$$
y=ax^3+bx^2+cx+d
$$
椭圆曲线和他们没有太大的区别。椭圆曲线和三次函数不同的地方在于等号左边是y的平方,这使得函数图像沿x轴对称:
$$
y^2 = x^3 + ax + b
$$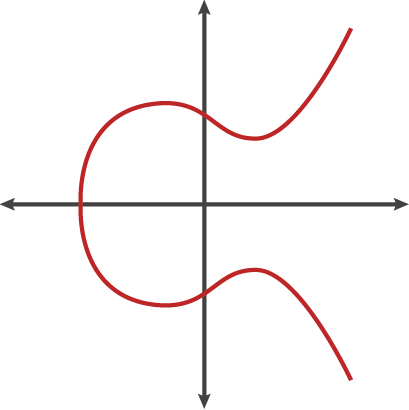
因为椭圆曲线的等号左边是y的平方,所以它也不像三次函数那样陡峭。此外,椭圆曲线可能是不想接的,如下图:
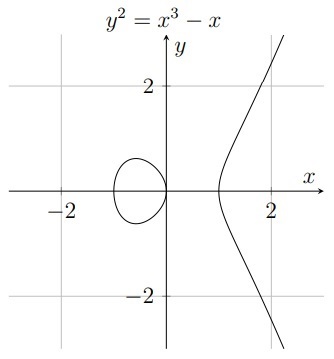
比如,比特币使用的椭圆曲线被称为secp256k1,使用下面的方程:
$$
y^2=x^3+7
$$
椭圆曲线的加法
过曲线上的两点A、B画一条直线,找到直线与椭圆曲线的交点,交点关于x轴对称位置的点,定义为A+B,即为加法。如下图所示:A + B = C
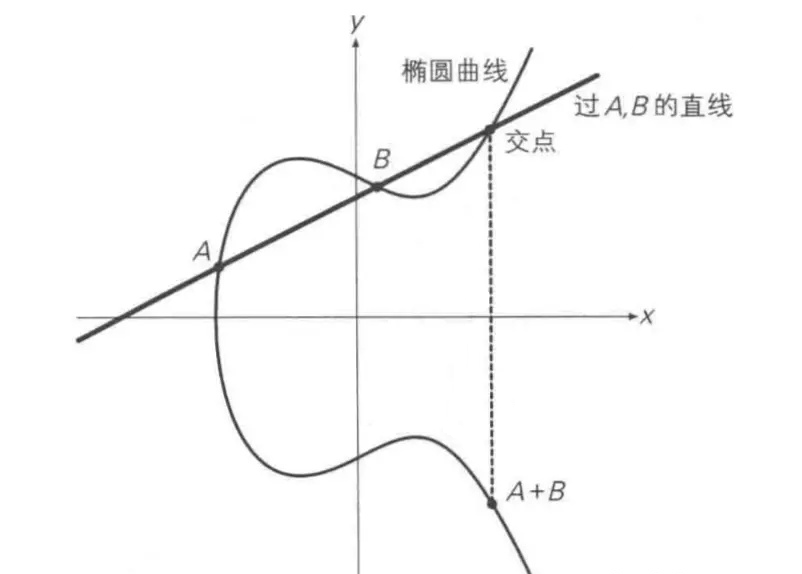
椭圆曲线因其点加法运算(point addition)而被广泛使用。
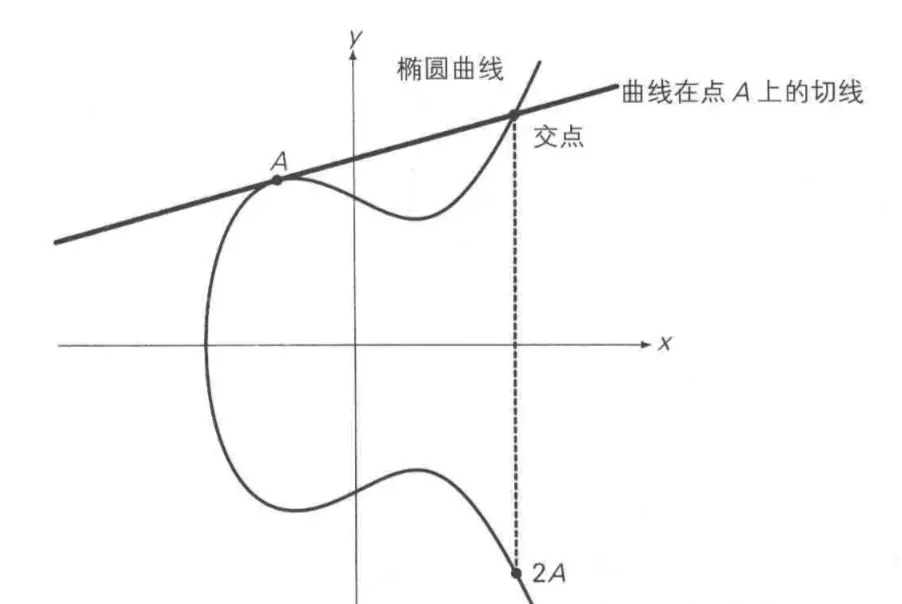
椭圆曲线的二倍运算
上述方法无法解释A + A,即两点重合的情况,因此在这种情况下,将椭圆曲线在A点的切线,与椭圆曲线的交点,交点关于x轴对称位置的点,定义为A + A,即2A,即为二倍运算。
同余运算
同余就是有相同的余数,两个整数 a、 b,若它们除以正整数 m所得的余数相等,则称 a,b对于模m同余。
$$
a≡b (mod m)
$$
有限域
椭圆曲线是连续的,并不适合用于加密,所以必须把椭圆曲线变成离散的点,要把椭圆曲线定义在有限域上。而椭圆曲线密码所使用的椭圆曲线是定义在有限域内,有限域最常见的例子是有限域GF(p),指给定某质数p,由0,1,2…,p-1共p个元素组成的整数集合中加法、二倍运算。例如GF(233)就是:
$$
y^2=(x^3+7) (mod 223)
$$
详见上一篇帖子。
乘法逆元
在模7乘法中:
- 1的逆元为1 (1*1)%7=1
- 2的逆元为4 (2*4)%7=1
- 3的逆元为5 (3*5)%7=1
- 4的逆元为2 (4*2)%7=1
- 5的逆元为3 (5*3)%7=1
- 6的逆元为6 (6*6)%7=1
数学解释
并不是所有的椭圆曲线都适合加密,上述是一类可以用来加密的椭圆曲线,也是最为简单的一类。
针对曲线Ep(a,b)表示为:
$$
y^2=x^3+ax+b(mod p), x,y \in [0,p],p为质数
$$
该曲线关于x轴对称。选择两个满足下列条件的小于p(p为素数)的非负整数a、b,要求满足以下条件:
$$
4a^3+27b^2≠0(mod p),a和b是小于p的非负整数
$$
1、有限域的负元
P(x,y)的负元是(x,-ymodp)=(x,p-y)
2、有限域的加法,P+Q
P(x1,y1),Q(x2,y2)和R(x3,y3)三点,其中R是PQ直线与曲线的交点的关于x轴的对称点,即 R=P+Q,有如下关系:
$$
x_3≡k^2-x_1-x_2(modp),y_3≡k(x_1-x_3)-y_1(modp)
$$
3、斜率计算
若P=Q,即计算P点切线,则
$$
k=(3x_2+a) \div (2y_1)
$$
若P≠Q,则
$$
k=(y_2-y_1) \div (x_2-x_1)
$$
椭圆曲线加解密算法原理
设私钥、公钥分别为d、Q,即Q = dG,其中G为基点,椭圆曲线上的已知G和dG,求d是非常困难的,也就是说已知公钥和基点,想要算出私钥是非常困难的。其中基点是椭圆曲线上选择的一个点,这个点能够保证满足dG=∞的最小正整数n足够大,也就是阶足够大。1<私钥<n,大于n的私钥必能在[1,n)中找到对应的私钥b使得aG=bG,换句话说也就是有足够多的私钥。
公钥加密:选择随机数r,将消息M生成密文C,该密文是一个点对,C = {rG, M+rQ},其中Q为公钥。
私钥解密:M + rQ - d(rG) = M + r(dG) - d(rG) = M,其中d、Q分别为私钥、公钥。
椭圆曲线签名算法原理
椭圆曲线签名算法(ECDSA)。设私钥、公钥分别为d、Q,即Q = dG,其中G为基点。
私钥签名:
- 选择随机数r,计算点rG(x, y)。
- 根据随机数r、消息M的哈希h、私钥d,计算s = (h + dx)/r。
- 将消息M、和签名{rG, s}发给接收方。
公钥验证签名:
- 接收方收到消息M、以及签名{rG=(x,y), s}。
- 根据消息求哈希h。
- 使用发送方公钥Q计算:hG/s + xQ/s,并与rG比较,如相等即验签成功。
原理:hG/s + xQ/s = hG/s + x(dG)/s = (h+xd)G/s = r(h+xd)G / (h+dx) = rG
签名过程
假设要签名的消息是一个字符串:“Hello World!”。DSA签名的第一个步骤是对待签名的消息生成一个消息摘要,不同的签名算法使用不同的消息摘要算法,而ECDSA256使用SHA256生成256比特的摘要。
摘要生成结束后,应用签名算法对摘要进行签名:
- 产生一个随机数k
- 利用随机数k,计算出两个大数r和s。将r和s拼在一起就构成了对消息摘要的签名。
这里需要注意的是,因为随机数k的存在,对于同一条消息,使用同一个算法,产生的签名是不一样的。从函数的角度来理解,签名函数对同样的输入会产生不同的输出。因为函数内部会将随机值混入签名的过程。
验证过程
关于验证过程,这里不讨论它的算法细节。从宏观上看,消息的接收方从签名中分离出r和s,然后利用公开的密钥信息和s计算出r。如果计算出的r和接收到的r值相同,则表示验证成功,否则,表示验证失败。